Insights
The virtue of transparency in prediction

What is the best way to form predictions from a data sample? This is a big question, but at its core lies a fundamental tension between explaining the past and anticipating the future.
August 2024
Predictions can fail by paying too little attention to the past (underfitting) or by paying too much attention (overfitting). High-complexity machine learning (ML) models address this problem by recombining past information in thousands (or millions) of exotic ways to map out generalized rules for any situation.
An alternative method, called relevance-based prediction (RBP), considers each situation one at a time, and extracts the past data that is most useful for that task. We show that there is a deep connection between the two approaches, but only relevance maintains the transparency that makes it easy to explain precisely how each past experience informs a prediction.
Key highlights
“Everything should be made as simple as possible, but no simpler.” This sentiment, typically attributed to Albert Einstein, nicely frames the concept of overfitting a data set. Data about the past is usually quite complicated because it reflects some legitimate patterns in addition to random noise. Finding a simpler explanation can separate the patterns from the noise. But for a given data set, how simple should we get?
Economists and statisticians have always prized simple models with focused sets of predictive variables because they are less easily fooled by spurious relationships. On the other hand, ML research has found that with the right techniques, avoiding overfitting requires more complexity, not less. One such technique is to generate thousands, or even millions, of random transformations of the available data and then condense the results using regularized regression.
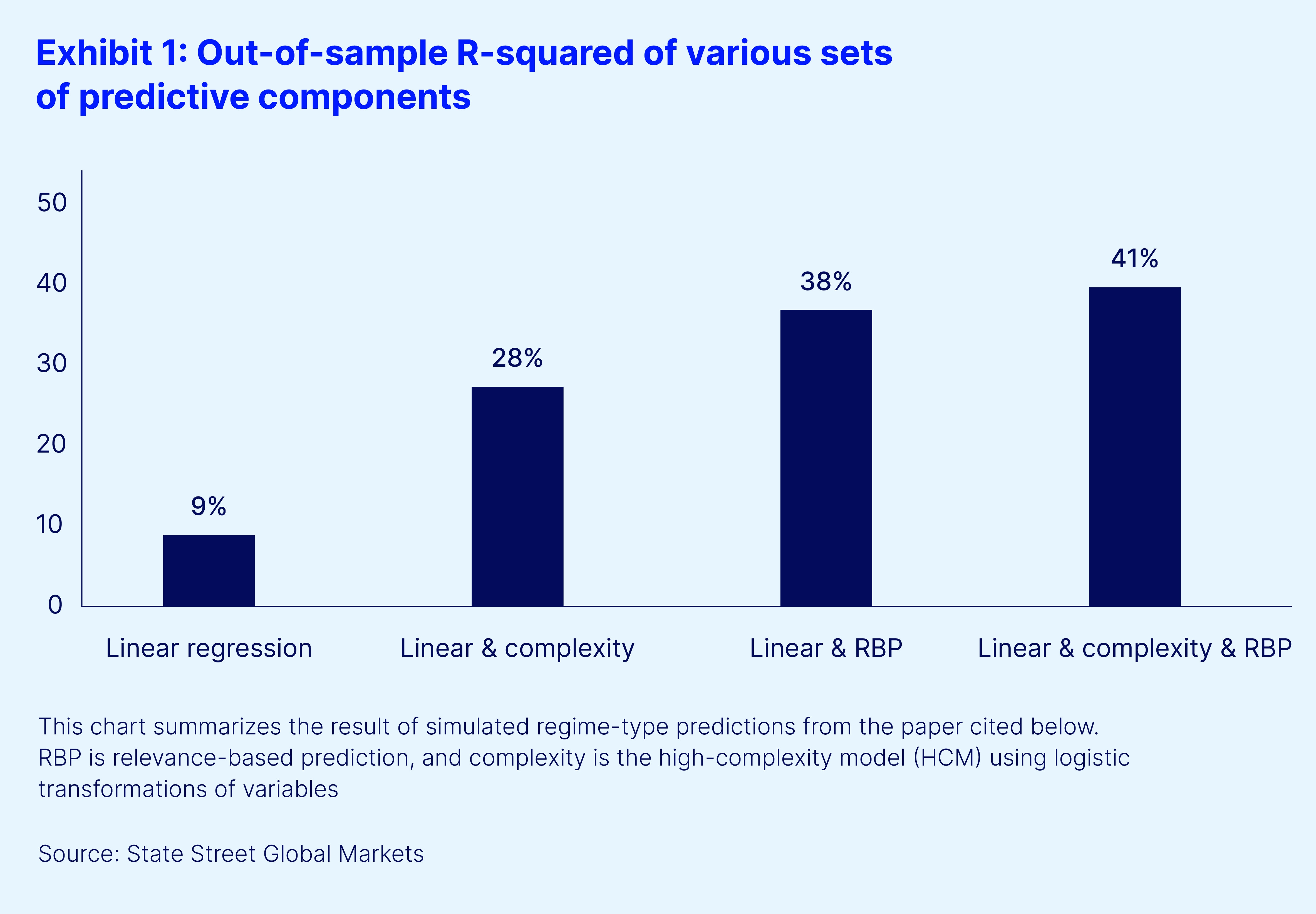
An alternative approach, RBP, identifies the blend of observations and variables that are most important for each prediction task. ML models need to be complex because they need to learn generalized rules that apply to every conceivable input. By contrast, RBP reasons through one task at a time, illustrating which data to focus on in each case.
It turns out that the high-complexity model and RBP identify much of the same information (see for example the summary in Exhibit 1, based on a regime-type simulation). This result is useful because it offers transparent insights into the workings of both approaches. Because RBP forms predictions as weighted averages of prior outcomes, we can take a new perspective on overfitting which is: How many observations are used to inform a given prediction, and how are they used?
Simplicity, then, applies not to the nature of the relationships we want to analyze, but to the method of how we do it. Transparency and interpretation bring great value to that process.



